コラム

---

１．ＡＢテストの歴史と仮説検証の必要性

ＡＢテストはオバマ元大統領の選挙キャンペーン（２００７年からの選挙活動の際）におけるサイト改善の施策で用いられ成功を収めて、特に有名になりました。
ＡＢテスト自体は１９００年代前半に始まり、最初はダイレクトメール（以下 ＤＭ）で利用された歴史があるテスト手法です。
当時は複数パターンのＤＭを試し、反応率のよいＤＭを送るといった手法に使われました。ここでのパターンとは「こういうＤＭなら反応してくれるであろう」という施策案のことです。

施策案は、説明が合理的で仮に立てた説をベースとした「仮説」のことです。
そしてＡＢテストにおいては、いくつかの仮説（複数パターン）の中からどの仮説の反応がよいか、しっかりと調べて事実を確認することになります。その作業が「検証」ですね。

つまりＡＢテストとは、仮説を検証しながら最適な施策を導き出すことなのです。その検証作業で仮説検定を行います。
仮説検定とは、単なるCV数やCVR等の数値の単純比較による多い、少ない、高い、低いではなく、データ数を統計を用いて、どちらに勝敗があるのかの判断をすることです。

---

２．ＡＢテストの検定

当社のＡＢテストツールＶＷＯでは、結果の判定にベイズ検定（ベイズ理論）を用いてＡＢテストの検定を行います。
トーマズベイズによるベイズの定理が発表された１７００年中頃から、その理論は存在しています。

その後、ベイズ統計の基礎となる考え方などが発表されました。
しかし最近まで、普及するような実用化には至りませんでした。
その一番の理由はマシンパワーがないと実用化が難しいという現実でした。

ＡＢテストの検定にベイズ検定が本格的に使われはじめたのも、ここ数年で最近のことです。それ以前は頻度統計による検定が使われてきました。

頻度統計におけるＡＢテストの検定にはカイ２乗検定、フィッシャーの正確確率検定、ニ項検定、ｔ検定などの方法があります。

ここではそれぞれの検定の説明は省略しますが、その中で汎用的に普及しているのはカイ２乗検定です。
なぜなら、ABテストの有意差を判定するために、カイ２乗検定は独立性の検定として利用でき、単純に差の有無を判定するだけでエクセル上で簡単に計算可能だからです。
そのためＡＢテストの検定として広く普及してきました。
今でもABテストでの有意差を判定するため、カイ２乗検定は身近な検定として用いられています。

次回はベイズ検定にも触れたいのですが、比較する意味でまず今回は、ＡＢテストの検定としてメジャーであるカイ２乗検定についての説明となります。

またカイ２乗検定について、どのようにしてその正否を統計的に判断（判定）していくのかを過去当社で実施したＶＷＯのＡＢテスト事例の数値を利用して解説していきます。

※ここでは、施策結果の良し悪しを議論するための説明を行うものではありません。

---

３．ＡＢテストでの有意性の計算

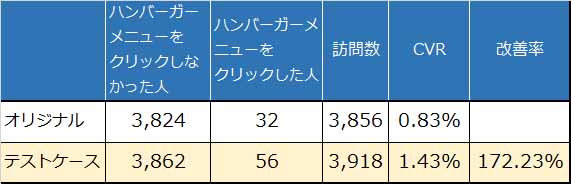
まず、以下のＡＢテストの施策を行った事例（図１）を使い、ABテストの有意差を判定するカイ２乗検定の結果を調べていきます。

図１．ＡＢテストの施策を行った事例（要素クリック：ハンバーガーメニュー）

最初のステップとして、期待値を計算します。
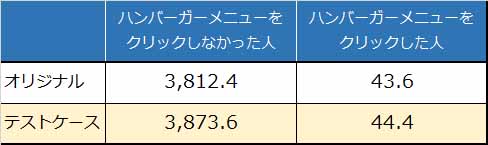
期待値の計算方法は以下のエクセルのとおりです。それぞれの期待値の計算結果を図２に示します。

図２．ＡＢテストの施策を行った事例に対する各期待値

エクセルによる各期待値の計算方法

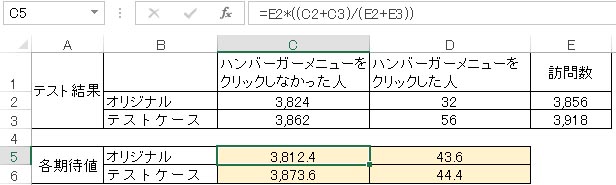
そして各カイ２乗値を計算（実測値から期待値を引いた値を2乗して期待値で割ったもの）した後、それらを足し合わせた結果が最終的なカイ２乗値となります。

図３．ＡＢテストの施策を行ったページの各カイ２乗値

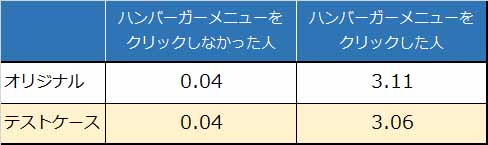
エクセルによる各カイ２乗値の計算方法

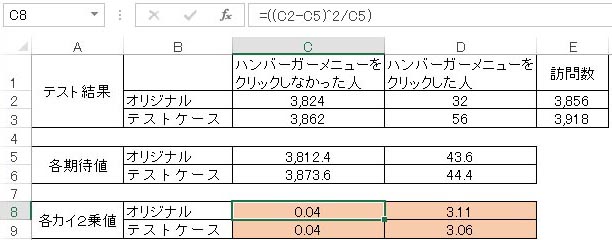
各カイ２乗値＝（テスト結果の値 － 期待値）²／　期待値

ＡＢテストの施策を行ったページ（要素クリック：ハンバーガーメニュー）の各カイ２乗値を足して、最終的なカイ２乗値は６．２５となりました。

カイ２乗値 ＝ 0.04 ＋ 0.04 ＋ 3.11 ＋ 3.06 ＝　６．２５

次に、最終的なカイ２乗値での判定結果を求めていきます。
その前に必要となる指標、自由度があります。計算方法は以下のとおりです。

自由度 ＝ （横の項目数 －１）×（縦の項目数 －１）

ＡＢテストの施策を行った事例（分割表）の自由度の計算式は
（横の項目数：２ －１）×（縦の項目数：２ －１）で、結果は１です。

※自由度とは縦・横で自由に決めることができる値の数です。
　この場合２行×２列となるため２では自由な値を取ないため、それぞれの行・列数から１を引いた値が自由度となります。
　またｎ行×ｍ列分割表での自由度の計算方法は、それぞれの行・列数を１引いた上で掛け合わせた数値となります。

この自由度とカイ２乗値分布により、有意差の検定（判定）を行っていきます。

カイ２乗値分布とは正規分布における変数に対し、変数の２乗和から導き出す分布のことで、理論値からの差異において確率的に表した分布です。

図４．カイ２乗値分布（自由度：１）

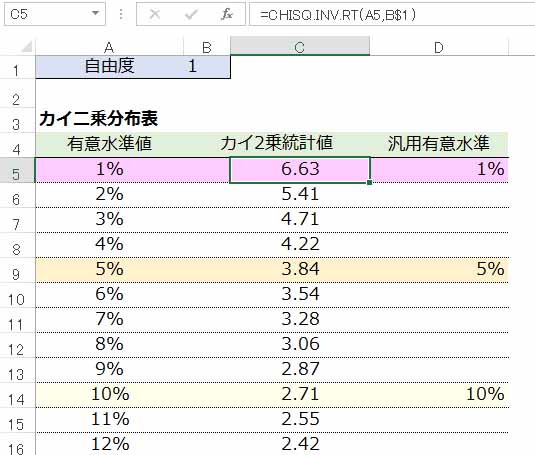
施策を行ったページに対するＡＢテスト（要素クリックＫＰＩ：ハンバーガーメニュー）のカイ２乗検定値は６．２５です。
カイ２乗値分布（自由度：１）と照合すると、ＡＢに差がある確率はどれくらいなのでしょうか。

図４のカイ２乗値分布（自由度：１）を見ると５％が３．８４で、１％が６．６３となっています。
結果の６．２５は、６．６３までは届かないが３．８４は超えているので５％有意と言えます。
（同じ結果ということは５％の確率でしか起こらない）

つまり９５％の確率で差が有ることになります。（１００回行った場合に９５回は差が出る）

その結果、このＡＢテストでは９５％の確率でテストバターン ＞ オリジナルの差が有るという結果になりました。

ところでABテストの有意差の％ですが、通常は５％有意を用います。
それより厳しい判断の１％有意や、緩い判断の１０％有意を用いるケースもあります。
またABテストの有意差、つまり有意性の観点から、１％刻みで起こりうる事象の確率を示す場合もあります。

---

４．まとめ

最後にABテストの有意差を判定する、カイ２乗検定は頻度統計（頻度データの評価）のひとつです。
エクセルで検定の計算をすることが出来ますので、作業面では便利に使えます。皆様も試してみてください。

ただし、頻度統計では設定する母集団を定数として、観測したデータを確率変数として扱います。
そのため、サンプル数が少ないと判定が出にくい面があると言われています。

ＶＷＯはベイズ検定（ベイズ統計）を利用しています。
今回使用したＡＢテストの事例におけるＶＷＯのベイズ検定結果は９９％でした。

次回はカイ２乗検定との比較もしつつ、「ベイズ検定」のことについて触れていきたいと思います。

---

【おすすめ情報】

　[必見]GoogleオプティマイズのABテストでの検定方法とその課題

　　　第二弾ではどんなことが語られるのか、乞うご期待！！

【ご質問やお問合せに関して】

また、googleアナリティクスに関するデータ分析や、多変量解析含む各種マーテケィングデータ分析などのサービスも行っております。
各種データ分析に関しても、お力添えさせていただきます。問合せ・ご相談のほど、よろしくお願いいたします。